This blogpost is my personnal writeup of the challenge Le Retour de Jafar that you can still play on Hackropole.
Analysis of the cipher
Let’s first breafly analyse the cipher. This cipher is a block cipher, following a construction called a Substitution Permutation Network. Here is some technical details :
- 128 bits of block size
- 3 parts for the encryption/decryption :
- 20 rounds of round key addition, substitution and permutation,
- A multiplication of the state at this point by the secret key in $\mathbb{F}_{2^{128}}$,
- Another 20 rounds of round key addition, substitution and permutation.
- No key schedule, the same key is repeated for each round
The goal of this challenge is to be able to forge a fresh and valid plaintext/ciphertext pair. To achieve this, we can ask three times for an encryption or a decryption of a choosen 16 bytes block.
Some details about this challenge are a bit unusual, we can ask for encryption and decryption, there quite a lot of rounds (40 + a multiplication in the middle) and we’re asking to be able to forge a fresh plaintext/ciphertext, but not to recover the key. This smells like a boomerang attack… I was conviced of that during the FCSC, but at some point I was blocked, and gave up, so this writeup is an upsolve of the challenge.
Notations
I will precise some notations that I will use during this writeup :
- $a\oplus b$ means the bitwise-XOR between $a$ and $b$,
- If $a, b \in \mathbb{F}_{2^n}$, then the XOR is just the addition in that field, that will be noted $a+b$,
- Let $E$ be a set, then $\sharp E$ is the cardinality of $E$,
- $\lbrace a, \ldots, b \rbrace$ is the set of all the integers between $a$ and $b$, both included.
- $\mathbb{P}(A)$ is the probability of $A$ to occur.
Solve
SBox analysis
When we are facing a symetric cipher, one of the first thing that I try is to analyse the SBox. There are some great tutorials about SBox analysing like this one that is based on sagemath, or directly the sagemath documentation of the module sage.crypto.sbox.SBox that is also a good resource.
Some tools are really usefull (you can check the documentation below to have a better understanding of it):
- DDT (Difference Distribution Table), it allows to detect if an SBox has some issues with differential cryptanalysis. More formaly $DDT(i,j) = \sharp \lbrace x\in\lbrace 0, \ldots, 255\rbrace, SBox(x \oplus i) = SBox(x) \oplus j\rbrace$ .
- LAT (Linear Approximation Table) that allows to detect linear relations between the input of the SBox and the output of it.
From these two tables, we can find interesting properties (there exists a lot more metrics and tables like the Boomerang Connectivity Table, but I will not use it for this solve). Furthermore, one can have a general visual representation of the LAT and DDT using the Jackson Pollock representation, but note that using only this visual representation, one may miss some critical information (p.e it may be tricky to spot a precise differential because of the colors used), that is why I recommand to also “analyse” it programmatically.
Let first check the DDT of the SBox in sage and the probabilities of the differentials:
from sage.crypto.sbox import SBox
S = SBox([
0x00, 0x6a, 0x60, 0x19, 0x1b, 0x22, 0x69, 0x43, 0x31, 0x7b, 0x59, 0x68, 0x03, 0x28, 0x51, 0x41,
0xb0, 0xfa, 0xd8, 0xe9, 0x82, 0xa9, 0xd0, 0xc0, 0x81, 0xeb, 0xe1, 0x98, 0x9a, 0xa3, 0xe8, 0xc2,
0x73, 0x48, 0x02, 0x42, 0x12, 0x10, 0x71, 0x49, 0x78, 0x23, 0x52, 0x1a, 0x62, 0x32, 0x72, 0x30,
0xf9, 0xa2, 0xd3, 0x9b, 0xe3, 0xb3, 0xf3, 0xb1, 0xf2, 0xc9, 0x83, 0xc3, 0x93, 0x91, 0xf0, 0xc8,
0x5e, 0x6f, 0x36, 0x7c, 0x56, 0x46, 0x04, 0x2f, 0x67, 0x1e, 0x07, 0x6d, 0x6e, 0x44, 0x1c, 0x25,
0xe6, 0x9f, 0x86, 0xec, 0xef, 0xc5, 0x9d, 0xa4, 0xdf, 0xee, 0xb7, 0xfd, 0xd7, 0xc7, 0x85, 0xae,
0x55, 0x1d, 0x7f, 0x24, 0x75, 0x37, 0x65, 0x35, 0x05, 0x45, 0x74, 0x4f, 0x76, 0x4e, 0x15, 0x17,
0x84, 0xc4, 0xf5, 0xce, 0xf7, 0xcf, 0x94, 0x96, 0xd4, 0x9c, 0xfe, 0xa5, 0xf4, 0xb6, 0xe4, 0xb4,
0x4b, 0x33, 0x29, 0x21, 0x20, 0x39, 0x01, 0x7a, 0x5b, 0x50, 0x63, 0x70, 0x0b, 0x53, 0x58, 0x4a,
0xda, 0xd1, 0xe2, 0xf1, 0x8a, 0xd2, 0xd9, 0xcb, 0xca, 0xb2, 0xa8, 0xa0, 0xa1, 0xb8, 0x80, 0xfb,
0x3b, 0x13, 0x08, 0x38, 0x79, 0x5a, 0x09, 0x61, 0x11, 0x0a, 0x2b, 0x40, 0x3a, 0x18, 0x6b, 0x2a,
0x90, 0x8b, 0xaa, 0xc1, 0xbb, 0x99, 0xea, 0xab, 0xba, 0x92, 0x89, 0xb9, 0xf8, 0xdb, 0x88, 0xe0,
0x64, 0x77, 0x5c, 0x57, 0x5f, 0x4d, 0x0c, 0x54, 0x2e, 0x26, 0x4c, 0x34, 0x06, 0x7d, 0x27, 0x3e,
0xaf, 0xa7, 0xcd, 0xb5, 0x87, 0xfc, 0xa6, 0xbf, 0xe5, 0xf6, 0xdd, 0xd6, 0xde, 0xcc, 0x8d, 0xd5,
0x2c, 0x47, 0x16, 0x0d, 0x6c, 0x2d, 0x3d, 0x1f, 0x0f, 0x3f, 0x3c, 0x14, 0x0e, 0x66, 0x7e, 0x5d,
0x8e, 0xbe, 0xbd, 0x95, 0x8f, 0xe7, 0xff, 0xdc, 0xad, 0xc6, 0x97, 0x8c, 0xed, 0xac, 0xbc, 0x9e
])
S.maximal_difference_probability()
# returns 1.0 i.e there is at least one difference with proba 1
We found something really interesting !
But wait, what a difference with a probability 1 means ? It means that there exists a tuple $(\delta,\Delta)\in\mathbb{F}_{2^8}$ such that : For all $x\in\mathbb{F}_{2^8}, S(x+\delta) = S(x) + \Delta$ . This also implies that the value of the DDT at $\delta, \Delta$ will be equal to 256.
Proof :
Let $x, \delta, \Delta \in \mathbb{F}_{2^8}$, then $P(S(x + \delta) = S(x) + \Delta) = \frac{DDT(\delta, \Delta)}{256}$. So, a differential pair $\lparen\delta, \Delta)$ that holds with a probability of 1 is equivalent to $DDT(\delta, \Delta) = 256$.
We can find the values $\delta, \Delta$ that have such property :
ddt = S.difference_distribution_table()
for i in range(256):
for j in range(256):
if ddt[i, j] == 256:
print(i,j)
We obtain three candidates : $\lparen24, 129), (74, 6)$ and $\lparen82, 134)$.
Round function differential
Now that we have three differentials with probability 1 for the SBox, then we can try to find a round differential such that the output of the round is also a differential for the next round. To speed up the process, I programmed it in Rust rather than python.
Note : Because we have 4 candidates for each of the 16 bytes block, we have a total of $4^{16} = 2^{32}$ possibilities, which is brute-forcable. You can find the Rust program at the end of the writeup (it basicaly tries every possible input differential and checks if the output differential is equal to the input one). One may use more sofisticated ways to find interesting round differentials, but the presented method has the avantage to be very straitforward.
Thanks to this program, found a candidate for what we are looking for (in hex, MSB first): 00524a18004a005252001818004a0000. I will show what it implies and why it is a serious issue.
Let write the round function $R = Permute \circ Sbox \circ Addkey$, then we just found $\delta_r$ such that for every possible input value $x$ of $R$, we have $Permute \circ Sbox (x\oplus\delta_r) = Permute \circ Sbox (x) \oplus \delta_r$. Lets prove that thanks to that, one can find a valid differential of probability 1 for an arbitraty number of rounds :
- The first step is to prove that if we have a valid differential pair $\lparen\delta, \Delta)$ for $Permute \circ Sbox$ then this is also a differential pair with probability 1 for $R = Permute \circ Sbox \circ Addkey$ :
Proof :
Let $\delta, \Delta \in \mathbb{F}_{2^8}$ such that $\forall x, S(x + \delta) = S(x) + \Delta$, let $x, k \in \mathbb{F}_{2^8}$ be resp. the input of the round function and the key, then $S((x+k)+\delta) = S(x+k) + \Delta$ because $x+k\in\mathbb{F}_{2^8}$. - Let assume that we have a found differential pair for the round function $R$ $\lparen\delta_r, \delta_r)$ with probability 1.0.
- By hypothesis, $\forall x \in \mathbb{F}_{2^{128}}, R(x+\delta_r) = R(x) + \delta_r$.
- Let assume that for $R^n$ (i.e $n$ compositions of the round function) we have a differential pair $\lparen\delta_r, \delta_r)$ with probability 1.0. Let $x \in \mathbb{F}_{2^{128}}$, then $R^{n+1}(x + \delta_r) = R(R^{n}(x + \delta_r)) = R(R^n(x) + \delta_r) = R^{n+1}(x) + \delta_r$ by hypothesis.
- Moreover, we also found a differential pair for the inverse of the round function.
Proof : Let $x \in \mathbb{F}_{2^{128}}$
$R(x + \delta_r) = R(x) + \delta_r\ \Leftrightarrow\ x + \delta_r = R^{-1}(R(x) + \delta_r)$
Because $R$ and $R^{-1}$ are bijections from $\mathbb{F}_{2^{128}}$ to itself, we can rewrite the last equality as $R^{-1}(y) + \delta_r = R^{-1}(y + \delta_r)$ (with $y \in \mathbb{F}_{2^{128}}$). - Using the same method as in step 2., one can show that this differential holds for an arbitrary number of inverse rounds.
Note that we are very lucky to find an input differential with the same output differential, otherwise we would have been forced to look for differentials that propagate over several rounds, which seems at first more complicated.
Boomerang attack
Principle
Okay, so what can we do now ? The goal of the challenge is to forge a valid plaintext/ciphertext pair, which does not necessary imply to recover the key. To achieve that, we have a round differential that progrates for an arbitrary number of rounds, and also for an arbitrary number of inverse rounds.
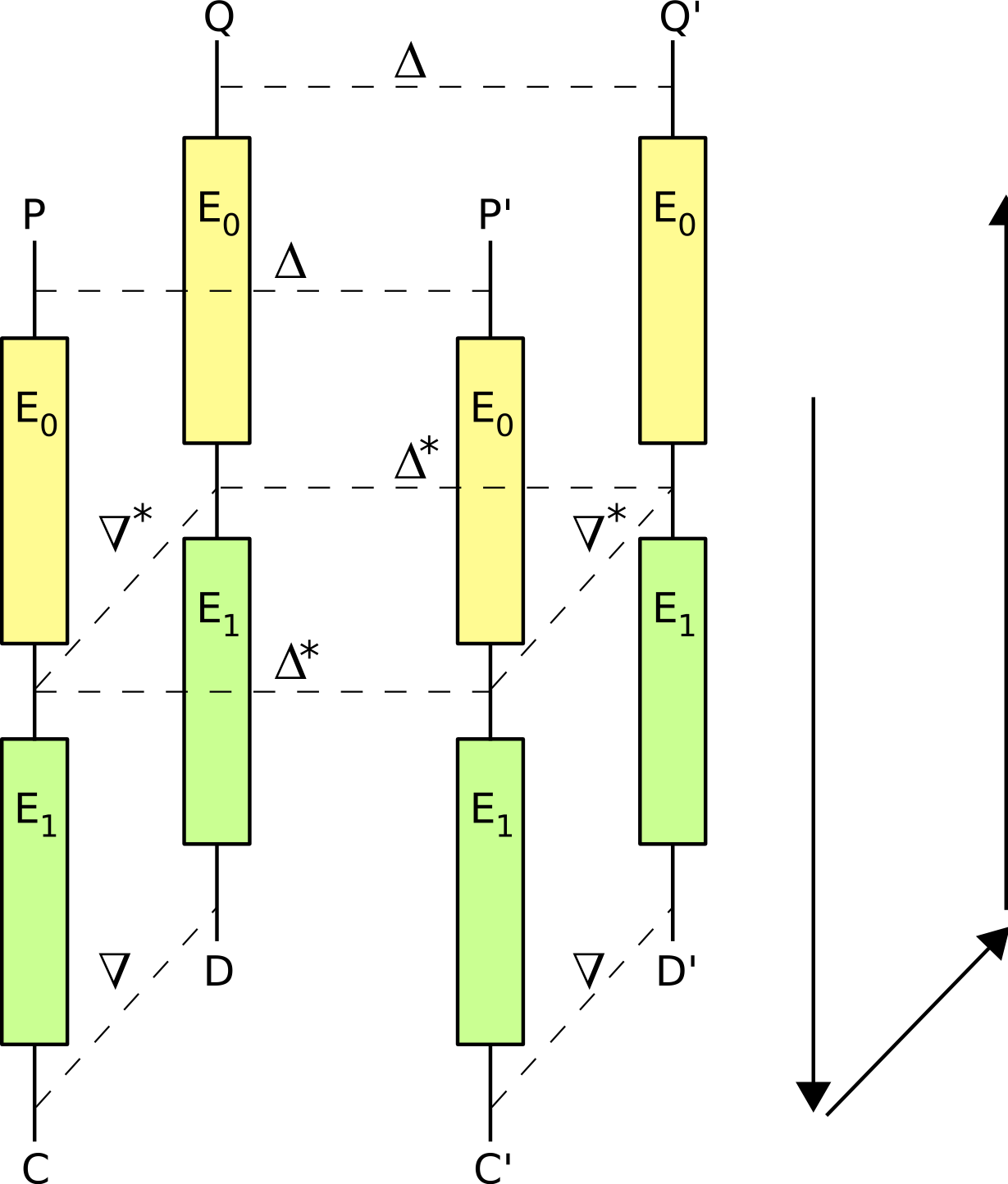
In fact, an attack seems really interesting : a boomerang attack. Here is a diagram of it (from the wikipedia page) :
 Credits : CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=523640
Credits : CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=523640
But why does a boomerang attack seems promising ?
- First of all, we can encrypt and decrypt data (which is not very common in CTF challenges), and we need both encryption and decryption to perform a boomerang attack.
- Moreover, because of the structure of the cipher and this “Middle” function that is just a multiplication of the state by the key in $\mathbb{F}_{2^{128}}$. This middle part is affine, which implies that it can satisfies the requirements about the differencies called $\Delta^\ast$ and $\nabla^\ast$ in the diagram below. The second effect of this middle part is that it stops the differential that propagates during the 20 previous rounds.
- Finally, $E_0$ showed in the diagram can be written here as the first $N$ rounds before the Middle part, and $E_1$ can be written as the middle part and the last $N$ rounds.
Note that one can also state that $E_0$ is made of the firsts $N$ rounds and the middle part, and $E_1$ is made of the lasts $N$ rounds, this is totaly equivalent, we will just have differents values for $\Delta^{\ast}$ and $\nabla^{\ast}$.
Perfect, so let’s proceed to get a new plaintext/ciphertext pair !
In practice
By following the notations of the diagram of the boomerang attack :
- I will choose a random $P$, ask for its encryption $C$ by the cipher, then ask for the decryption $Q$ of $D = \delta_r \oplus C$.
- Then I will ask for the encryption $C’$ of $P’ = P \oplus \delta_r$.
- Then using the boomerang property, I know that the decryption of $C’ \oplus \delta_r$ will be equals to $Q \oplus \delta_r$.
Let’s put that in a python script :
from pwn import *
DELTA_R = 0x00524a18004a005252001818004a0000
# in local because I didn't succeed to solve during the CTF
r = remote("localhost", 4000)
r.recvuntil(b">>>")
# ask for encryption
P = b"PleaseTheFlag!!!"
r.sendline(b"enc")
r.recvuntil(b">>>")
r.sendline(P.hex().encode())
# The result is at the second line, in hex
C = bytes.fromhex(r.recvuntil(b">>>").decode().split("\n")[1])
# ask for decryption
D = (DELTA_R ^ int.from_bytes(C)).to_bytes(16, "big")
r.sendline(b"dec")
r.recvuntil(b">>>")
r.sendline(D.hex().encode())
Q = bytes.fromhex(r.recvuntil(b">>>").decode().split("\n")[1])
P_prime = (int.from_bytes(P) ^ DELTA_R).to_bytes(16, "big")
r.sendline(b"enc")
r.recvuntil(b">>>")
r.sendline(P_prime.hex().encode())
C_prime = bytes.fromhex(r.recvuntil(b">>>").decode().split("\n")[1])
# Now we can deduce a new plaintext/ciphertext valid pair
ciphertext = (int.from_bytes(C_prime) ^ DELTA_R).to_bytes(16, "big")
plaintext = (int.from_bytes(Q) ^ DELTA_R).to_bytes(16, "big")
r.sendline(plaintext.hex())
r.recvuntil(b">>>")
r.sendline(ciphertext.hex())
r.recvall()
# Congrats! Here is the flag:
# FCSC{41858b8f2b39df5ec1af02e581195b8b1c91135619d60092fce00a93775858cf}
We got the flag ! I would like to thanks graniter and more generaly all the FCSC team for creating such challenges !
Rust source code
use std::io::stdout;
use std::io::Write;
// SBox
const S: [u8; 256] = [
0x00, 0x6a, 0x60, 0x19, 0x1b, 0x22, 0x69, 0x43, 0x31, 0x7b, 0x59, 0x68, 0x03, 0x28, 0x51, 0x41,
0xb0, 0xfa, 0xd8, 0xe9, 0x82, 0xa9, 0xd0, 0xc0, 0x81, 0xeb, 0xe1, 0x98, 0x9a, 0xa3, 0xe8, 0xc2,
0x73, 0x48, 0x02, 0x42, 0x12, 0x10, 0x71, 0x49, 0x78, 0x23, 0x52, 0x1a, 0x62, 0x32, 0x72, 0x30,
0xf9, 0xa2, 0xd3, 0x9b, 0xe3, 0xb3, 0xf3, 0xb1, 0xf2, 0xc9, 0x83, 0xc3, 0x93, 0x91, 0xf0, 0xc8,
0x5e, 0x6f, 0x36, 0x7c, 0x56, 0x46, 0x04, 0x2f, 0x67, 0x1e, 0x07, 0x6d, 0x6e, 0x44, 0x1c, 0x25,
0xe6, 0x9f, 0x86, 0xec, 0xef, 0xc5, 0x9d, 0xa4, 0xdf, 0xee, 0xb7, 0xfd, 0xd7, 0xc7, 0x85, 0xae,
0x55, 0x1d, 0x7f, 0x24, 0x75, 0x37, 0x65, 0x35, 0x05, 0x45, 0x74, 0x4f, 0x76, 0x4e, 0x15, 0x17,
0x84, 0xc4, 0xf5, 0xce, 0xf7, 0xcf, 0x94, 0x96, 0xd4, 0x9c, 0xfe, 0xa5, 0xf4, 0xb6, 0xe4, 0xb4,
0x4b, 0x33, 0x29, 0x21, 0x20, 0x39, 0x01, 0x7a, 0x5b, 0x50, 0x63, 0x70, 0x0b, 0x53, 0x58, 0x4a,
0xda, 0xd1, 0xe2, 0xf1, 0x8a, 0xd2, 0xd9, 0xcb, 0xca, 0xb2, 0xa8, 0xa0, 0xa1, 0xb8, 0x80, 0xfb,
0x3b, 0x13, 0x08, 0x38, 0x79, 0x5a, 0x09, 0x61, 0x11, 0x0a, 0x2b, 0x40, 0x3a, 0x18, 0x6b, 0x2a,
0x90, 0x8b, 0xaa, 0xc1, 0xbb, 0x99, 0xea, 0xab, 0xba, 0x92, 0x89, 0xb9, 0xf8, 0xdb, 0x88, 0xe0,
0x64, 0x77, 0x5c, 0x57, 0x5f, 0x4d, 0x0c, 0x54, 0x2e, 0x26, 0x4c, 0x34, 0x06, 0x7d, 0x27, 0x3e,
0xaf, 0xa7, 0xcd, 0xb5, 0x87, 0xfc, 0xa6, 0xbf, 0xe5, 0xf6, 0xdd, 0xd6, 0xde, 0xcc, 0x8d, 0xd5,
0x2c, 0x47, 0x16, 0x0d, 0x6c, 0x2d, 0x3d, 0x1f, 0x0f, 0x3f, 0x3c, 0x14, 0x0e, 0x66, 0x7e, 0x5d,
0x8e, 0xbe, 0xbd, 0x95, 0x8f, 0xe7, 0xff, 0xdc, 0xad, 0xc6, 0x97, 0x8c, 0xed, 0xac, 0xbc, 0x9e
];
// Permutation
const P: [u8; 128] = [
0x77, 0x65, 0x02, 0x3a, 0x4a, 0x7f, 0x17, 0x57, 0x66, 0x62, 0x5a, 0x6d, 0x7c, 0x20, 0x0b, 0x14,
0x63, 0x76, 0x71, 0x0f, 0x78, 0x0e, 0x0c, 0x4b, 0x5f, 0x09, 0x2d, 0x3b, 0x18, 0x60, 0x73, 0x00,
0x51, 0x6c, 0x58, 0x1d, 0x28, 0x50, 0x08, 0x13, 0x44, 0x38, 0x29, 0x26, 0x40, 0x4d, 0x42, 0x64,
0x07, 0x34, 0x31, 0x01, 0x7e, 0x1a, 0x12, 0x4c, 0x10, 0x2b, 0x56, 0x49, 0x70, 0x7b, 0x21, 0x16,
0x1c, 0x23, 0x69, 0x79, 0x06, 0x3d, 0x37, 0x3c, 0x0d, 0x6f, 0x1f, 0x36, 0x2e, 0x45, 0x75, 0x05,
0x46, 0x74, 0x41, 0x04, 0x48, 0x4e, 0x0a, 0x47, 0x03, 0x2a, 0x59, 0x67, 0x7a, 0x22, 0x5e, 0x25,
0x3e, 0x4f, 0x5c, 0x2f, 0x7d, 0x5d, 0x33, 0x39, 0x11, 0x2c, 0x53, 0x55, 0x68, 0x3f, 0x72, 0x27,
0x35, 0x6e, 0x6b, 0x30, 0x43, 0x15, 0x54, 0x24, 0x6a, 0x19, 0x1b, 0x52, 0x61, 0x32, 0x5b, 0x1e
];
// Successive power of 2 until 2^128, just to speed up a bit
const Power: [u128; 128] = [
1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192, 16384, 32768, 65536, 131072, 262144,
524288, 1048576, 2097152, 4194304, 8388608, 16777216, 33554432, 67108864, 134217728, 268435456,
536870912, 1073741824, 2147483648, 4294967296, 8589934592, 17179869184, 34359738368, 68719476736,
137438953472, 274877906944, 549755813888, 1099511627776, 2199023255552, 4398046511104, 8796093022208,
17592186044416, 35184372088832, 70368744177664, 140737488355328, 281474976710656, 562949953421312,
1125899906842624, 2251799813685248, 4503599627370496, 9007199254740992, 18014398509481984,
36028797018963968, 72057594037927936, 144115188075855872, 288230376151711744, 576460752303423488,
1152921504606846976, 2305843009213693952, 4611686018427387904, 9223372036854775808, 18446744073709551616,
36893488147419103232, 73786976294838206464, 147573952589676412928, 295147905179352825856,
590295810358705651712, 1180591620717411303424, 2361183241434822606848, 4722366482869645213696,
9444732965739290427392, 18889465931478580854784, 37778931862957161709568, 75557863725914323419136,
151115727451828646838272, 302231454903657293676544, 604462909807314587353088, 1208925819614629174706176,
2417851639229258349412352, 4835703278458516698824704, 9671406556917033397649408, 19342813113834066795298816,
38685626227668133590597632, 77371252455336267181195264, 154742504910672534362390528,
309485009821345068724781056, 618970019642690137449562112, 1237940039285380274899124224,
2475880078570760549798248448, 4951760157141521099596496896, 9903520314283042199192993792,
19807040628566084398385987584, 39614081257132168796771975168, 79228162514264337593543950336,
158456325028528675187087900672, 316912650057057350374175801344, 633825300114114700748351602688,
1267650600228229401496703205376, 2535301200456458802993406410752, 5070602400912917605986812821504,
10141204801825835211973625643008, 20282409603651670423947251286016, 40564819207303340847894502572032,
81129638414606681695789005144064, 162259276829213363391578010288128, 324518553658426726783156020576256,
649037107316853453566312041152512, 1298074214633706907132624082305024, 2596148429267413814265248164610048,
5192296858534827628530496329220096, 10384593717069655257060992658440192, 20769187434139310514121985316880384,
41538374868278621028243970633760768, 83076749736557242056487941267521536, 166153499473114484112975882535043072,
332306998946228968225951765070086144, 664613997892457936451903530140172288, 1329227995784915872903807060280344576,
2658455991569831745807614120560689152, 5316911983139663491615228241121378304, 10633823966279326983230456482242756608,
21267647932558653966460912964485513216, 42535295865117307932921825928971026432, 85070591730234615865843651857942052864,
170141183460469231731687303715884105728];
// Apply SBox on each byte of the state
fn sub(input: u128) -> u128 {
let mut output = 0u128;
for i in (0..128).step_by(8) {
output += (S[((input >> i) & 0xff) as usize] as u128)<< i;
}
output
}
// Bit permutation of the state
// this is the bottleneck of the program in terms of speed
fn permute(input: u128) -> u128 {
(0..128).map(|i| (((input & Power[i]) != 0) as u128) << P[i])
.sum()
}
// Round function
fn round(input: u128) -> u128 {
permute(sub(input))
}
fn main() {
let mut stdout = stdout();
// Potential values of the input differential
let in_diff: [u8; 4] = [0, 24, 74, 82];
// 16 bytes, 4 possible diff per byte : 4^16 i.e 2^32 possibilities
for i in 0usize..4294967296usize {
// Sometimes print the percentage of tested candidates
if i % 500000 == 0 {
print!("\r{:?}", (i as f64)/4294967296f64 * 100.0);
stdout.flush().unwrap();
}
// Compute the candidate for the round differential
let mut round_diff: u128 = 0;
for k in (0..32).step_by(2) {
round_diff += (in_diff[((i>>k) & 0b11) as usize] as u128) << (k*4);
}
// Check if the input equals to the output
if round(round_diff) == round_diff {
println!("");
println!("Found ! {:?}", round_diff);
}
}
}